Using trigonometry can solve many problems precisely where you may have only been able to approximate before. Trigonometry is used extensively in everything from engineering to architecture to G.P.S, business, surveying, navigation, astronomy and physical sciences. Before going to the solution of trigonometry equations, you might like to read about trigonometry equations and trigonometric functions.

What is trigonometry and trigonometric equations?
The word TRIGONOMETRY (combination of Greek words), TRI that means THREE, GON that means SIDES and METRON that means measure. So, trigonometry is an important branch of mathematics that studies the triangles and the relationship between their sides and the angles between their sides. In simple words, it means measurement of triangle.
Equations that involves the trigonometric functions are called trigonometric equations. Solving a trigonometric equation and an algebraic equation, such as finding the value of variable that satisfy the equation, is almost similar. Trigonometric functions are mainly three sin, cos and tan etc.
Trigonometric functions:
The six trigonometric functions for any acute angle of a right-angle triangle ABC as shown in figure as you know trigonometry deals with right angles. The right-angle triangle is the one with an angle of 90. The opposite side of the right angle is called hypotenuse. The other two sides are adjacent and opposite.


What is Solution of a triangle?
As we’ve discussed a triangle has six important factors; three angles and three sides. If any of three of these six elements, out of which at least one side, are given the remaining three elements can be determined. These unknown elements can be fin out by a method called solution of a triangle. So, in the solution of triangles, we may encounter certain problems involving angle of measures, heights and distances, angle of elevation and depression, oblique triangles and area of triangles etc. And here, our main concern is to find out the area of triangle by using calculators.
Triangle area formula
Area of a triangle is the total space covered by all three side of the triangle. In simple mathematical questions we use the following formula to find out the area.

Where b represents the base and h represents the height of the triangle. But, in trigonometry, the rule for finding the area is slightly different because trigonometry concerns about the measurements of the angles.
For example
If you have a triangle with a base measuring 4 cm long, and a height measuring 8 cm long. We will put these given values in to the formula to get the answer.
Formula for the area of a triangle.
As you already know the formula:
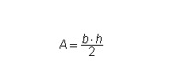
Here, b is the length of the triangle’s base, and h is the height of the triangle.
By putting lengths of the base and height into the formula.
Multiply the two values together, then divide their product by 2. You would get the area of the triangle in square units.

There are number of equations for calculating the area of triangles in trigonometry, all of them based on the required information in question. Three of them, are given below
- Area of triangle in terms of the measure of two sides and their included angle.
- Area of triangle in terms of the measure of one side and two angles.
- Area of the triangle in terms of the measures of its sides which is also known as hero’s formula.
Above these three methods of finding area of a triangle, the third one solving by using hero’s formula along with simple triangle area formula can be calculated by using online calculators.
Hero’s formula:
Hero’s formula is used to find the area of triangle when the lengths of all sides is known. The formula is credited to Hero of Alexandria who was Greek engineer and mathematician. Basically, it is used to find out area of any triangle on the basis of the three sides lengths a, b, and c.

Here, a, b and c are the lengths of the triangle and s is semi perimeter which is equals to the half of the sum of all three sides.

Firstly, you would find the value of semi perimeter, then put the values of all three lengths of the triangle into the formula to get the answer.
Online calculators for area of triangle:
Area calculator for a triangle help students to find out the area of a triangle in single click.
There are number of online websites available which provides free tools for calculating the area of triangles in trigonometry. Either we calculate the area of triangle by using simple formula or hero’s formula, these calculators provide their services to get the solution in a quick way. We use different equations to find the area in trigonometry and it largely depends upon the information that are we provided with.
Some of the recommended online calculator websites that provides free tools for students to find the area calculations are given here;
All these websites have triangle area calculator which will you to learn and compose trigonometric operations without any trouble. Simply, they can help to find the area of triangle by both ways, simple way and by hero’s formula. Moreover, these websites are the cheapest means of calculations and they are way easy to use.
How to use area calculator:
These online tools show two calculators for triangle area calculation either by simple triangle area formula or hero’s formula.
Triangle area calculator
Let’s suppose you know the two sides of a triangle, height and base and the angle between them. All you have to do is
·Enter the length or height
It is for example equals to 8cm.
·Put the second triangle side or base
Let’s suppose it is 5cm.
·Determine the angle between these two sides
For example, 30 degrees.
·triangle area calculator will show the answer after all calculations.
The area of triangle would be equal to 20cm2.
Same is the way you can use the hero’s formula calculator to calculate the area of the triangle.
Conclusion:
Thus, these online tools of area calculators not only save a lot of time as there is no need to write a formula to get the answer, but they are much easier to use as well. Also, they are money-saving so anyone can take advantage of them by just clicking on the keyboard. And these calculators are not just tools for the use of students but engineers, astronomers, physical and social scientists and pretty much everyone who deals with trigonometry
